Structured Machine Learning
Total Variation
The use of machine-learning in neuroimaging offers new perspectives in early diagnosis and prognosis of brain diseases. Although such multivariate methods can capture complex relationships in the data, traditional approaches provide irregular (l2 penalty, see SVM in first row in the figure below) or scattered (l1 penalty, see Lasso in third row in the figure below) predictive pattern with a very limited relevance. A penalty like Total Variation (TV) that exploits the natural 3D structure of the images can increase the spatial coherence of the weight map (see SVM+TV and Lasso+TV in second and fourth rows in the figure below). The versatility of our framework authorizes its application to all kind of structured input data. Without any modification of the algorithm we have analysed the 2D surface-based, cortical thickness (see right columns if the figure). However, TV penalization leads to non-smooth optimization problems which disables classical gradient descent methods.
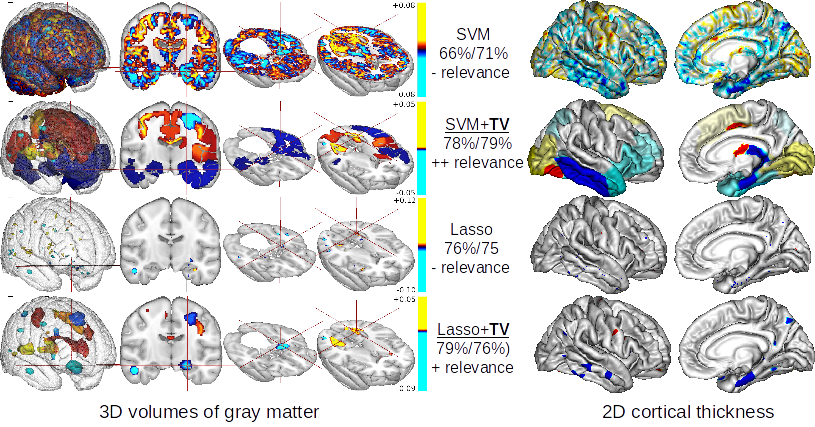
Predictive map of different algorithms obtained with patients that will convert to Alzheimer Disease vs healthy controls. Left column:3D voxel-based of grey matter. Right column weights on 2D Cortical thickness. First row: the state-of-the-art SVM leads to a “christmas tree” effect with a poor relevance. On the second row we added our spatial constraint (TV-penalty). Weights map provide a clear view of the medial-temporal atrophy. The third row shows the map obtained with the state-of-the-art Lasso algorithm. The weights map is too sparse and hardly interpretable. On the fourth row we added our spatial constraint (TV-penalty) which lead to a more interpretable map of biomarkers.
Optimization
Within the BrainOmics team at NeuroSpin, we developed an optimization framework that minimizes any combination of l1, l2, and TV penalties while preserving the exact l1 penalty. This algorithm uses Nesterov's smoothing technique to approximate the TV penalty with a smooth function such that the loss and the penalties are minimized with an exact accelerated proximal gradient algorithm. We propose an original continuation algorithm that uses successively smaller values of the smoothing parameter to reach a prescribed precision while achieving the best possible convergence rate. This algorithm (CONESTA: COntinuation with NEsterov smoothing in a Shrinkage Thresholding Algorithm) can be used with other losses or penalties.
ParsimonY: Sparse and Structured Machine Learning Libray in Python
With The BrainOmics team, we produced a library (https://github.com/neurospin/pylearn-parsimony) based on the python language that implements many structured machine learning algorithms. The first stable release is scheduled by mid May 2014.